POTENZA E VELOCITÀ NEL CANOTTAGGIO
I corpi che si muovono nei fluidi rallentano a causa delle
forze di resistenza.
Ciò rappresenta in realtà un trasferimento di quantità di moto dal corpo al fluido: il fluido circostante accelera mentre il corpo rallenta, quindi la quantità di moto totale rimane costante.
Una barca che si muove in fluido qual è l’acqua è soggetta
a vari tipi di resistenza:
- Resistenza superficiale , dovuta all'attrito tra lo scafo e
l'acqua che vi si trascina dentro;
- Resistenza di forma , dovuta alla turbolenza creata dal
passaggio dello scafo;
- Resistenza delle onde , dovuta all'energia persa durante la
creazione delle onde.
Gli scafi di canottaggio fuori scalmo, sono insoliti in
quanto la resistenza superficiale è la principale fonte di resistenza (circa
l'80%).
Per la maggior parte delle altre imbarcazioni, la resistenza delle onde domina. Anche l'aria contribuisce alla resistenza totale ma con una densità circa 1.000 volte inferiore all’acqua il suo contributo è decisamente meno gravoso (l'aria è solo un altro fluido).
Mentre il contributo dell'aria ferma è solo una piccola
percentuale della resistenza totale, la velocità dell'aria è molto più
variabile, quindi il contributo può incrementarsi notevolmente in caso di forti
venti contrari. Tutto ciò è dovuto al fatto che le resistenze fluido dinamiche
sono funzione del quadrato della velocità quindi un raddoppio di velocità si
traduce in un aumento di 4 volte la resistenza.
Inoltre essendo la potenza pari alla Forza x la velocità,
la dipendenza della potenza dal cubo della velocità P=k X V3
ha un'importante conseguenza quando si considera la potenza
richiesta per mantenere una velocità media dell’imbarcazione
Se un equipaggio ha per un tempo t una velocità di 4 m/s, e
poi per lo stesso tempo t 6 m/s, la distanza totale che percorrono è t x 4 + t
x 6 = (10 X t ) metri. Dall'equazione, assumendo k = 1 kg/m per
semplificare i calcoli, il lavoro totale W richiesto
(= potenza x tempo) è
W1=1
X 43 X t + 1 X 63 X t = t X (43 +63)
Joule
e la potenza media nei due
minuti (= lavoro/tempo) è di t (43 +63) /2 X t [Watt]
Supponiamo che lo stesso equipaggio abbia una velocità costante, di 5 m/s. La
distanza percorsa sarà 5 *2t =10 t
metri, come il caso precedente, ma questa volta l'energia totale richiesta è
diversa
W2 = t X (53 +53) Joule
W1/W2= t X (43 +63)
/ t X (53 +53)= (43 +63)/ (53 +53)=1,12
Cioè il
lavoro nel caso 1 è maggiore del 12 % rispetto a quello prodotto nel caso 2 e corrispondentemente,
avrà utilizzato per percorrere lo stesso spazio nello stesso tempo meno potenza
media 125/140 ovvero l’89% della potenza del caso 1
Ciò significa che è più
efficiente dal punto di vista energetico mantenere lo la velocità più costante
possibile durante una gara piuttosto che, ad esempio, iniziare velocemente e
rallentare, o iniziare lentamente e accelerare.
Ma, poiché la potenza assorbita, sia idrodinamica che aerodinamica, dipende dal cubo della velocità dello scafo, piuttosto che dalla velocità del centro di massa totale, gli stessi argomenti si applicano alla variazione della velocità dello scafo durante una ciclo di voga.
Se lo scafo in un ciclo di colpo viaggia 4 m/s per metà del
tempo e a 6 m/s per l’altra metà, sarà meno efficiente dello scafo che mantiene
la velocità costante a 5 m/s (si ottiene esattamente la stessa risposta di cui
sopra se si considera non più il tempo di un minuto ma il tempo in cui si
compie il ciclo di voga.
Pertanto è assolutamente indesiderabile avere troppe
variazioni nella velocità dello scafo durante il colpo (caratterizzato da prue
o poppe che “ballano il valzer” eccessivamente.
Del resto le imbarcazioni con scalmi mobili avevano
esattamente questo scopo, diminuire gli spostamenti delle masse dell’equipaggio
sull’imbarcazione e mantenere il più possibile ridotte le differenze tra
velocità massima e minima.
Detto ciò forse, più che concentrarsi sull’andamento delle
accelerazioni sarebbe importante concentrarsi sui valori massimi e minimo delle
velocità mantenendo il più vicino alla media
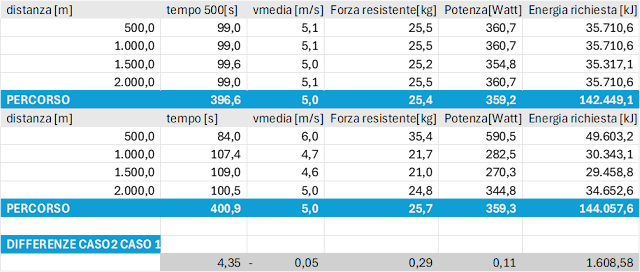
UN ESEMPIO PRATICO
In questo esempio a
parità di potenza media espressa il primo percorso viene completato in 4,35
secondi in meno del secondo. la Potenza è stata calcolata con la formula
individuata anche per il calcolo della potenza espressa da un atleta sul
remoergometro Concept2 P=2,8 X v3



Commenti
Posta un commento